Sine meaning – The sine function, a cornerstone of trigonometry, has a rich history and diverse applications across fields like calculus, physics, and engineering. Join us as we delve into its meaning, properties, and practical uses, unveiling the captivating world of sine.
From its origins in ancient civilizations to its modern-day significance, the sine function has played a pivotal role in shaping our understanding of mathematics and the world around us.
Historical Evolution of Sine
The sine function has a rich and extensive history, with contributions from mathematicians and cultures across the globe. The concept of sine emerged in ancient civilizations, with early evidence found in Babylonian and Indian texts dating back to the 2nd millennium BCE.
These texts employed geometric methods to calculate trigonometric ratios, including sine, for practical applications such as astronomy and surveying.In the Hellenistic era, Greek mathematicians like Hipparchus and Ptolemy developed sophisticated trigonometric tables, incorporating the sine function. The term “sine” itself is derived from the Latin translation of the Arabic word “jiba,” meaning “bay” or “gulf,” which referred to the vertical distance from the horizontal axis to a point on a circle.
Mathematical Definition and Properties
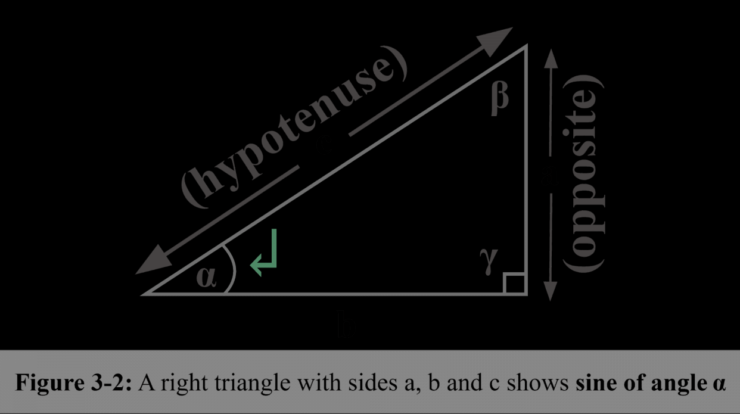
The sine function is mathematically defined as the ratio of the length of the opposite side to the length of the hypotenuse in a right triangle. It can also be expressed using the unit circle as the ratio of the y-coordinate of a point on the circle to its radius.The
sine function possesses several key properties, including:
- Periodicity: The sine function repeats itself every 2π units, or 360 degrees.
- Amplitude: The maximum value of the sine function is 1, and the minimum value is -1.
- Symmetry: The sine function is an odd function, meaning it is symmetric about the origin.
Applications in Trigonometry
The sine function plays a crucial role in solving trigonometric problems. It is used to find the unknown sides and angles of right triangles, a fundamental skill in fields such as surveying, navigation, and engineering. The sine function is also employed in calculating ratios of sides in oblique triangles using the Law of Sines.
Applications in Calculus
In calculus, the sine function is used extensively. Its derivative is the cosine function, and its integral is the negative cosine function. The sine function is applied in calculating velocities, accelerations, and wave motions. It is also used to model periodic phenomena, such as the oscillation of a pendulum or the propagation of sound waves.
Applications in Physics and Engineering: Sine Meaning
The sine function finds numerous applications in physics and engineering. In acoustics, it is used to describe the vibrations of sound waves. In electrical circuits, it is used to analyze alternating currents and impedances. The sine function is also employed in modeling periodic phenomena, such as the rotation of a wheel or the oscillations of a spring.
Visual Representation and Graphs
The sine function can be graphically represented as a wave. The graph of the sine function is a smooth, continuous curve that oscillates between1 and 1. The amplitude of the wave is 1, and the period is 2π units. The phase shift of the wave determines the horizontal displacement of the graph along the x-axis.
Outcome Summary
In conclusion, the sine function stands as a testament to the power of mathematics to describe and predict the intricacies of our universe. Its versatility and ubiquity continue to inspire discoveries and drive innovation across a wide range of disciplines.
Query Resolution
What is the sine function?
The sine function is a mathematical function that describes the vertical coordinate of a point on a unit circle as an angle is measured from the positive x-axis.
How is the sine function used in trigonometry?
The sine function is used to solve trigonometric problems involving angles and side lengths of triangles, such as finding the height of a building or the distance to a star.
What are some applications of the sine function in calculus?
The sine function is used in calculus to find the derivatives and integrals of functions, which are essential for understanding concepts like velocity and acceleration.






